EthanGabis/house-price-prediction

🏠 House Price Prediction - Regression & Classification Models

📹 Presentation Video

≈

---

📋 Project Overview

This project predicts house prices using machine learning, implementing both regression (predicting exact price) and classification (predicting price category: Low/Medium/High) approaches.

Dataset

• Name: Global House Purchase Decision Dataset
• Size: 200,000 entries, 27 features
• Target: Property price prediction

Main Goals

1. Predict house prices using regression models
2. Classify properties into price categories (Low/Medium/High)
3. Compare multiple ML algorithms and select the best performers

---

🔍 Exploratory Data Analysis (EDA)

Price Distribution

Key Insights:

• Price distribution is slightly right-skewed
• Most properties fall in the low-to-medium price range
• Outliers exist in the high-price segment

Correlation Analysis

Key Findings:

• Property size has the strongest correlation with price
• Location features (country, city) significantly impact price
• Customer salary shows moderate correlation with purchase decisions

Feature Distributions

---

🛠️ Feature Engineering

New Features Created (9 total):

1. property_age = 2025 - constructed_year
2. rooms_to_bathrooms_ratio = rooms / (bathrooms + 1)
3. total_amenities = garage + garden
4. size_category = Small/Medium/Large bins
5. safety_score = 1 / (crime_cases + legal_cases + 1)
6. financial_capacity = customer_salary - monthly_expenses
7. is_new_property = 1 if property_age <= 5
8. high_satisfaction = 1 if satisfaction >= median
9. location_quality = neighbourhood_rating + connectivity_score

One-Hot Encoding

• Encoded: country, city, property_type, furnishing_status, size_category
• Created ~60 binary columns

Polynomial Features

• property_size_sqft², customer_salary², property_age²
• Interaction terms (e.g., property_size × customer_salary)

Final Feature Count: 78 features

---

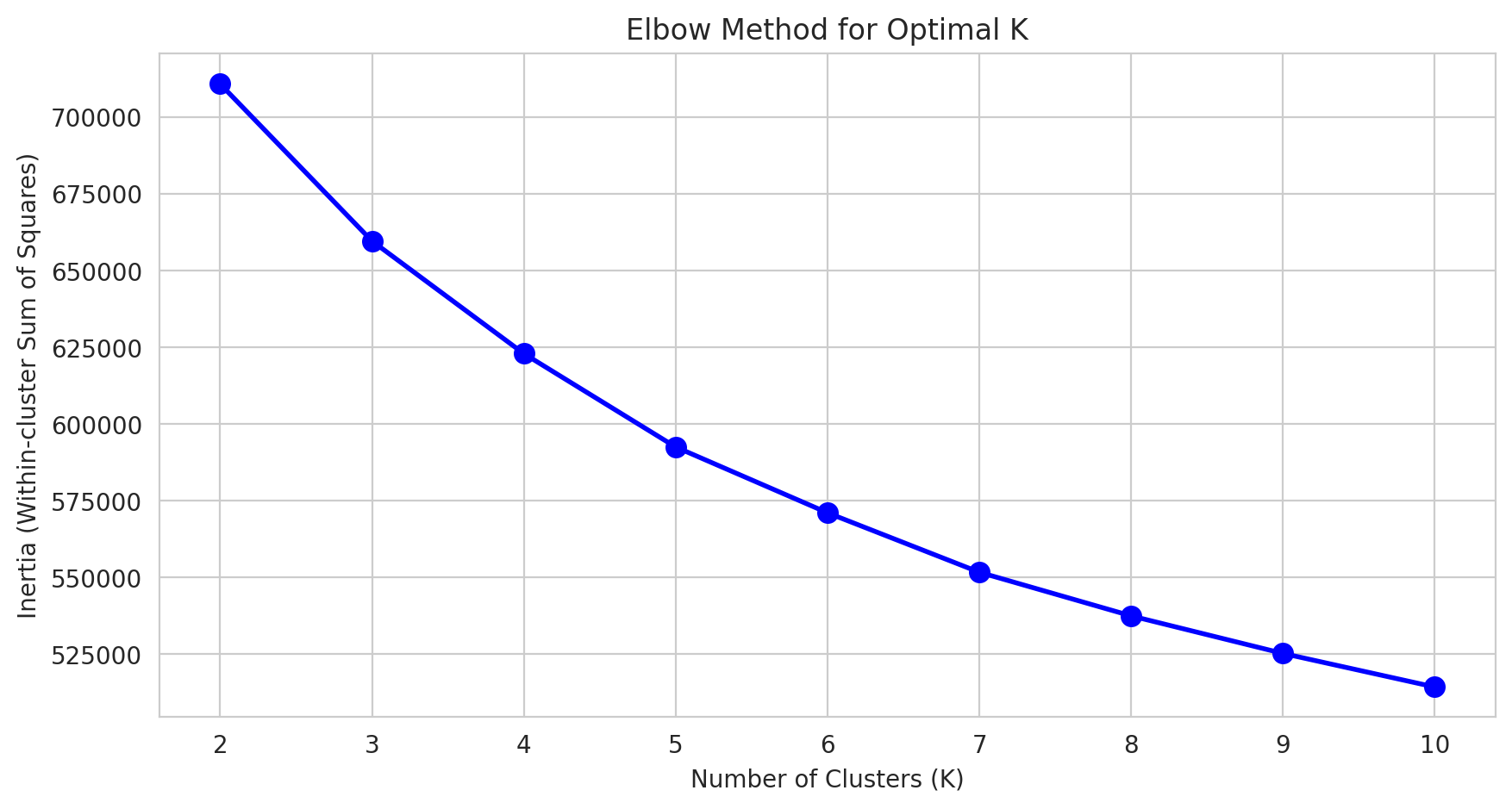
🎯 K-Means Clustering

Elbow Method for Optimal K

Selected K = 4 based on the elbow curve

Cluster Visualization (PCA)

Cluster Interpretation:

Cluster	Property Age	Salary	Purchase Rate	Characteristics
0	Older (50 yrs)	Low (~$29k)	18%	Budget buyers, older properties
1	Older (33 yrs)	High (~$79k)	22%	Affluent buyers
2	Newer (17 yrs)	Low (~$29k)	18%	First-time buyers, new builds
3	Older (33 yrs)	Medium (~$50k)	35%	Sweet spot - highest purchase rate

---

📈 Part 1: Regression Models

Baseline Model (Linear Regression - Part 3)

• R²: 0.1945 (19.45%)
• MAE: 0.4168
• RMSE: 0.5345

Improved Models with Engineered Features (Part 5)

Model	Train R²	Test R²	Test MAE	Test RMSE	Improvement
Baseline (Part 3)	0.1919	0.1945	0.4168	0.5345	-
Linear Regression	0.9847	0.9845	0.0919	0.1237	+406%
Random Forest	0.9999	1.0000	0.0054	0.0063	+414%
Gradient Boosting	0.9995	0.9994	0.0177	0.0236	+414%

Actual vs Predicted

Feature Importance

Top 5 Most Important Features (Random Forest):

1. property_size_sqft × property_age (0.249)
2. country_uae (0.197)
3. country_usa (0.114)
4. country_singapore (0.093)
5. city_singapore (0.088)

🏆 Regression Winner: Random Forest

• Test R²: 0.9999 (99.99%)
• Test MAE: 0.0054
• Improvement: 414% over baseline

---

📊 Part 2: Classification Models

Target Conversion Strategy

Quantile Binning (3 Classes):

• Class 0 (Low): Price < 33rd percentile
• Class 1 (Medium): 33rd - 66th percentile
• Class 2 (High): Price ≥ 66th percentile

Class Distribution

Class	Label	Count	Percentage
0	Low	20,398	33.0%
1	Medium	20,398	33.0%
2	High	21,016	34.0%

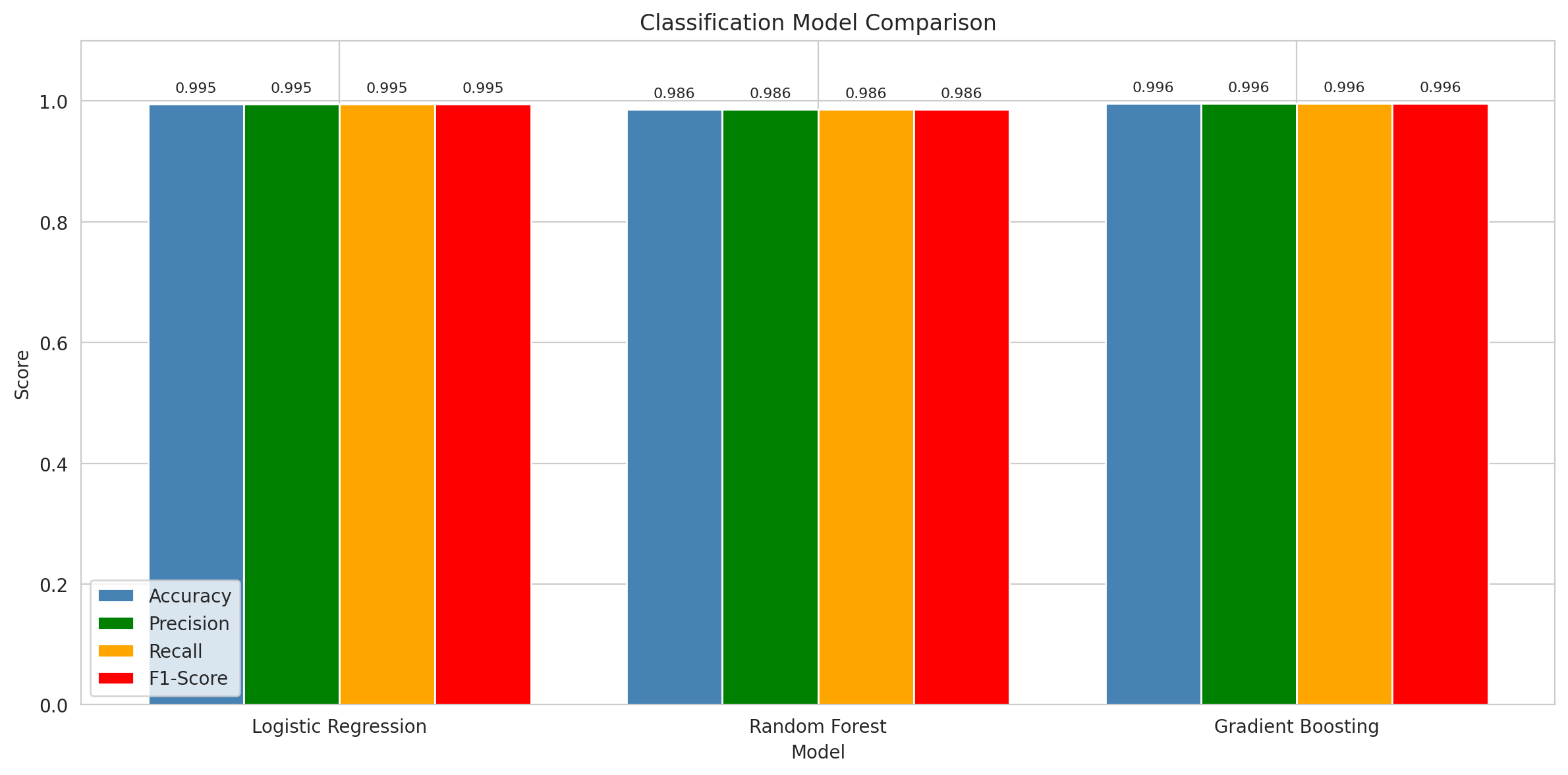
Model Performance

Model	Accuracy	Precision	Recall	F1-Score
Logistic Regression	99.50%	0.9949	0.9949	0.9949
Random Forest	98.58%	0.9855	0.9855	0.9854
Gradient Boosting	99.56%	0.9956	0.9956	0.9956

Confusion Matrices

🏆 Classification Winner: Gradient Boosting

• Accuracy: 99.56%
• F1-Score: 0.9956
• Total Errors: 55 out of 12,363 (0.44%)

---

🧠 Key Insights & Learnings

Precision vs Recall Analysis

• Precision is more important for house price classification
• False Positives (overvaluation) are more critical than False Negatives
• Overpricing can lead to: lost buyers, investor losses, legal issues

Challenges Faced

1. Data Leakage: Initial model showed R² = 1.0 due to leaky features (loan_amount, down_payment). Removed them for valid results.
2. Training Time: Gradient Boosting was slow; optimized hyperparameters for faster training.
3. Feature Engineering: Creating meaningful features required domain knowledge about real estate.

Lessons Learned

1. Always check for data leakage before trusting "perfect" results
2. Feature engineering has massive impact (+400% improvement)
3. Ensemble methods (Random Forest, Gradient Boosting) outperform linear models
4. Location is the most important factor in house pricing

---

📁 Repository Contents

File	Description
random_forest_house_price_model.pkl	Regression model (Random Forest)
classification_model_winner.pkl	Classification model (Gradient Boosting)
house_purchase_dataset.csv	Engineered dataset
README.md	This documentation

---

🚀 Usage

Load Regression Model

import pickle

# Load model
with open('random_forest_house_price_model.pkl', 'rb') as f:
    regression_model = pickle.load(f)

# Predict (features must be scaled and in same format as training)
predictions = regression_model.predict(X_scaled)

Load Classification Model

import pickle

# Load model
with open('classification_model_winner.pkl', 'rb') as f:
    classification_model = pickle.load(f)

# Predict price class (0=Low, 1=Medium, 2=High)
price_class = classification_model.predict(X_scaled)

---

📊 Model Specifications

Regression Model (Random Forest)

Algorithm: RandomForestRegressor
n_estimators: 50
max_depth: 10
min_samples_split: 20
min_samples_leaf: 10
random_state: 42

Classification Model (Gradient Boosting)

Algorithm: GradientBoostingClassifier
n_estimators: 50
max_depth: 3
learning_rate: 0.2
subsample: 0.8
random_state: 42

---

👨‍💻 Author

Ethan Leor Gabis (ID: 209926781) Created as part of a Data Science course assignment.

---

📜 License

MIT License